


Next: INTRODUCTION
Up: uiuc_thesis
Previous: Contents
Contents
- Illustration of the fracture process associated with the Titan IV SRMU grain collapse accident (taken from Chang et al., (1994)).
- CVFE concept showing one 4-node cohesive element between two linear-strain triangular volumetric elements. The cohesive element is shown in its deformed configuration. In its undeformed configuration is has no thickness and the adjacent nodes are superposed.
- Bilinear cohesive failure law for the pure tensile or mode I (
, left) and pure shear or mode II (
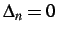 , right) cases. An unloading and reloading path is also shown in the mode I case.
, right) cases. An unloading and reloading path is also shown in the mode I case.
- Coupled cohesive failure model described by Equation 2.4; variation of normal (top) and shear(bottom) cohesive tractions with respect to normal (
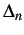 ) and tangential (
) and tangential (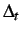 ) displacement jumps.
) displacement jumps.
- Time step defined by: (a) element size or (b) element type.
- Subcycling region distribution.
- Time step assignment.
- (a) Standard 1-D mesh. (b) 1-D mesh with inserted cohesive node.
- 2-D Cohesive element representation.
- 2-D cohesive element insertion: (a) proposed edge for cohesive insertion, (b) inserted cohesive element, (c) ``criss-crossed'' cohesive element.
- Connectivity update of nodes and elements.
- Common 2-D insertion cases.
- Illustrative example of three cohesive element insertions using Cases #2 and #3 in Figure 2.11.
- Illustration of insertion Case #5 in Figure 2.11.
- 1-D ``blind'' insertion test problem.
- 1-D ``blind'' insertion test problem: evolution of the displacement jump across the cohesive element (i.e., between nodes
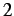 &
& 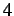 in Figure 2.14) resulting from a cohesive element insertion at time 0,
in Figure 2.14) resulting from a cohesive element insertion at time 0,
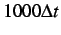 (
(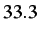
 ),
),
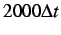 (
(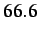
 ).
).
- Schematic representation of a damped 1-D cohesive element.
- Effect of cohesive damping: evolution of the displacement jump across the cohesive element for the simple 1-D test problem shown in Figure 2.14 and resulting from ``blind'' cohesive element insertion with damping at time 0,
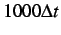 (
(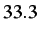
 ) and
) and
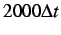 (
(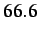
 ).
).
- 1-D cohesive element pre-stretching concept.
- 1-D cohesive element pre-stretching concept, with the pre-stretch applied equally on the two nodes.
- 2-D separation contributions from neighboring cohesive elements.
- 1-D test problem separation oscillations of nodes
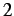 &
& 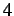 (Figure 2.14)
resulting from insertion with pre-stretching at time 0,
(Figure 2.14)
resulting from insertion with pre-stretching at time 0,
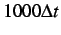 (
(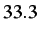
 ),
),
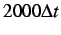 (
(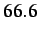
 ).
).
- Bounding box method.
- Multiple active cohesive regions.
- Stress-based insertion results for simple angled case.
- Simple CVFE mesh.
- Partitioned CVFE mesh.
- Reference problem in 1-D.
- x-t diagram in 1-D.
- Analytical solution for displacement , velocity
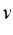 and stress
and stress
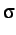 in the middle of the beam for the 1-D wave problem described in
Figure 3.1.
in the middle of the beam for the 1-D wave problem described in
Figure 3.1.
- Subcycling test described by Smolinski (1989) by Case
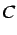 .
.
- Velocity profile of node
 with subcycling parameter
with subcycling parameter
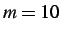 .
.
- Velocity profile of node
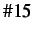 with subcycling parameter
with subcycling parameter
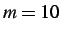 .
.
- Velocity profile of node
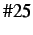 with subcycling parameter
with subcycling parameter
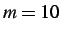 .
.
- Subcycling effect on (a) displacements and (b) velocities at node
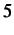 .
.
- Test case used to get timing results for subcycling.
- Nodes 12 through 20 are made cohesive.
- Velocity profile of node
 resulting from blind insertion at the
resulting from blind insertion at the  time step (
time step (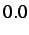
 ).
).
- Velocity profile of node
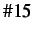 resulting from blind insertion at the
resulting from blind insertion at the 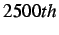 time step (
time step (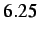
 ).
).
- Velocity profile of node
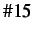 resulting from blind insertion at the
resulting from blind insertion at the 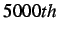 time step (
time step (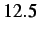
 ).
).
- Velocity profile of node
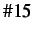 resulting from blind insertion at the
resulting from blind insertion at the 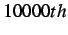 time step (
time step (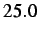
 ).
).
- Velocity profile of node
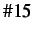 resulting from blind insertion with damping at the
resulting from blind insertion with damping at the 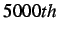 time step (
time step (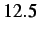
 ).
).
- Velocity profile of node
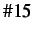 resulting from blind insertion with damping at the
resulting from blind insertion with damping at the 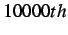 time step (
time step (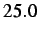
 ).
).
- Velocity profile of node
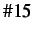 resulting from insertion with pre-stretching at the
resulting from insertion with pre-stretching at the 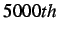 time step (
time step (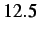
 ).
).
- Velocity profile of node
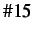 resulting from insertion with pre-stretching at the
resulting from insertion with pre-stretching at the 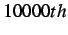 time step (
time step (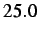
 ).
).
- Cohesive separation for node
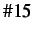 resulting from blind insertion at
resulting from blind insertion at 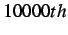 time step (
time step (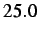
 )
)
- Cohesive separation for node
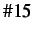 resulting from insertion with pre-stretching at
resulting from insertion with pre-stretching at 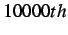 time step (
time step (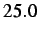
 )
)
- Test case for dynamic cohesive node insertion with pre-stretching.
- Test case for dynamic insertion with subcycling.
- Velocity profile of node
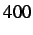 of dynamic cohesive node insertion at time step
of dynamic cohesive node insertion at time step 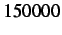 (
(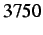
 ) with nodal subcycling using
) with nodal subcycling using
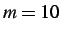 .
.
- Cohesive element distribution.
- Nodal displacements of a random node ahead of the notch for a problem with an equal region ratio () with subcycling parameters of
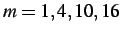 and
and 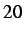 .
.
- Nodal displacements of a random node for the
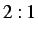 region ratio with subcycling parameters of
region ratio with subcycling parameters of
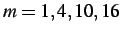 and
and 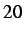 .
.
- Nodal displacements of a random node for the
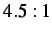 region ratio with subcycling parameters of
region ratio with subcycling parameters of
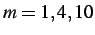 and
and 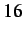 .
.
- Percent time savings vs region ratio for various subcycling parameters.
- Simple 2-D meshes with three cohesive elements inserted along (a) "horizontal" and (b) "mixed" interfaces.
- Normalized average stress levels for the volumetric elements of the middle cohesive element. Vertical lines at the
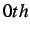 (
(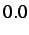
 ),
), 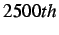 (
(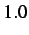
 ) and
) and 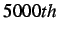 (
(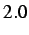
 ) time step represent dynamic insertion times.
) time step represent dynamic insertion times.
- Normalized separation of the tracking node for "horizontal" blind insertion at the
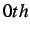 (
(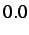
 ),
), 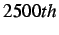 (
(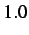
 ) and
) and 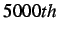 (
(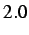
 ) time step.
) time step.
- Normalized separation of the tracking node for "mixed" blind insertion at the
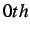 (
(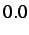
 ),
), 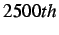 (
(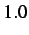
 ) and
) and 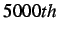 (
(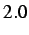
 ) time step.
) time step.
- Normalized separation of the tracking node for "horizontal" blind insertion with damping at the
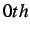 (
(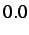
 ),
), 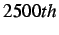 (
(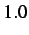
 with
with
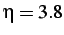 ) and
) and 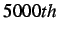 (
(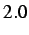
 with
with
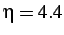 ) time step.
) time step.
- Normalized separation of the tracking node for "mixed" blind insertion with damping at the
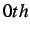 (
(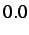
 ),
), 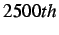 (
(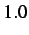
 with
with
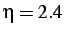 ) and
) and 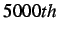 (
(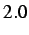
 with
with
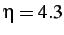 ) time step.
) time step.
- Normalized separation of the tracking node for ``horizontal'' insertion with with pre-stretching at the
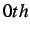 (
(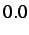
 ),
), 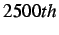 (
(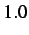
 ) and
) and 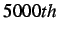 (
(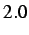
 ) time step.
) time step.
- Normalized separation of the tracking node for ``mixed'' insertion with with pre-stretching at the
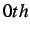 (
(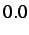
 ),
), 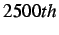 (
(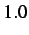
 ) and
) and 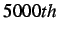 (
(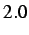
 ) time step.
) time step.
- Effect of blind insertion vs pre-stretching on the amplitude of the traction oscillations for increasing stress insertion levels, for the ``horizontal'' and ``mixed'' cases.
- Schematic of a mode I crack problem.
- Number of cohesive elements present in the domain over time for bounding box insertion.
- Mode I case crack tip distance versus time.
- Mode I reference case with cohesive elements present from the beginning of the simulation (10x exaggeration).
- Mode I bounding box solution (10x exaggeration) (edge key: thin = normal edge, dark = cohesive element, dashed = failing cohesive element, bold = failed cohesive element).
- Schematic representation of L-angle test specimen with boundary conditions.
- Number of cohesive elements present in the domain over time for various stress insertion levels.
- L-angle case crack tip distance versus time, for various stress insertion levels.
- L-angle reference case with cohesive elements present from the beginning of the simulation (10x exaggeration).
- L-angle case with stress based cohesive element insertion for a 15% stress level (10x exaggeration) (edge key: thin = normal edge, dark = cohesive element, dashed = failing cohesive element, bold = failed cohesive element).
- L-angle case with stress based cohesive element insertion for a 30% stress level (10x exaggeration).
- L-angle case with stress based cohesive element insertion for a 45% stress level (10x exaggeration) (edge key: thin = normal edge, dark = cohesive element, dashed = failing cohesive element, bold = failed cohesive element).
- Schematic representation of interface test specimen with boundary conditions.
- Deformation after 5000 time steps for stress insertion of 45% (10x exaggeration).
- Deformation after 17500 time steps for stress insertion of 45% (10x exaggeration).
- Deformation after 25500 time steps for stress insertion of 45% (10x exaggeration) (edge key: thin = normal edge, dark = cohesive element, dashed = failing cohesive element, bold = failed cohesive element).
- Schematic representation of interface test specimen with boundary conditions.
- Crack length history for a weak 60 degree interface.
- Crack speed history for a weak 60 degree interface.
- Mode I crack trapped along the weak Loctite-384 interface for a 45% stress-based insertion (no exaggeration) (edge key: thin = normal edge, dark = cohesive element, dashed = failing cohesive element, bold = failed cohesive element).
- Mode I crack trapped along the strong Weldon-100 interface for a 45% stress based insertion (no exaggeration) (edge key: thin = normal edge, dark = cohesive element, dashed = failing cohesive element, bold = failed cohesive element).
- Close-up of crack region along a weak interface (no exaggeration).
- Close-up of crack region along a strong interface (no exaggeration).
- L-angle reference case with cohesive elements inserted every (a) 100 time steps (b) 500 time steps at the 30% stress level (10x exaggeration).
- L-angle reference case with cohesive elements inserted every (a) 1000 time steps (b) 10000 time steps at the 30% stress level (10x exaggeration) (edge key: thin = normal edge, dark = cohesive element, dashed = failing cohesive element, bold = failed cohesive element).
- Number of cohesive elements present over time for insertion intervals of 100, 500, 1000, 5000 and 10000.
- Close-up of the three intervals presented in Figure 4.40.
- Schematic of a mode I crack problem using nodal subcycling and dynamic stress insertion of
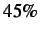 .
.
- Region ratio over time for the subcycling solutions with
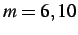 and
and 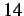 .
.
- Reference solution with cohesive elements present everywhere in the domain at the beginning of the simulation. No subcycling is used (10x exaggeration).
- (a) Solution having only dynamic insertion at 45% of the local stress with no subcycling. (b) Combined dynamic insertion with subcycling,
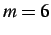 (10x exaggeration).
(10x exaggeration).
- (a) Combined dynamic insertion with subcycling,
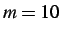 (b) Combined dynamic insertion with subcycling,
(b) Combined dynamic insertion with subcycling, 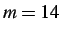 (10x exaggeration) (edge key: thin = normal edge, dark = cohesive element, dashed = failing cohesive element, bold = failed cohesive element).
(10x exaggeration) (edge key: thin = normal edge, dark = cohesive element, dashed = failing cohesive element, bold = failed cohesive element).
- Speedup results for L-angle case using 1, 2, 4, and 6 processors.
- Adaptive crack propagation.
- 11th element broken into 7 pieces.
- Velocity profile for new node #26 after element break up at time step 10000.
Mariusz Zaczek
2002-10-13