


Next: Cohesive Element Pre-Stretching
Up: Cohesive Element Stability and
Previous: Cohesive Element Stability and
Contents
One possible approach to reduce the potentially detrimental
oscillations associated with the "blind" insertion of cohesive
elements involve the introduction of some form of damping in the
cohesive response. Schematically, this approach corresponds to adding
a dash-pot in the cohesive element description
(Figure 2.16).
Figure 2.16:
Schematic representation of a damped 1-D cohesive element.
|
|
In its simplest form, the "damped" cohesive element response can be
characterized by a multiplicative term
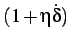 to
the cohesive failure law described in Section 2.1, with
to
the cohesive failure law described in Section 2.1, with 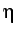 denoting the damping coefficient,
denoting the damping coefficient,
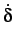 , the norm of the
velocity jump vector.
, the norm of the
velocity jump vector.
To illustrate the effect of this additional damping term on the
response of the inserted cohesive element, we reconsider the simple
1-D problem described in Figure 2.14. As shown in
Figure 2.17, the introduction of a damping term
in the cohesive element response eliminates all oscillations after
just a few time steps. However, it was found that the amount of
damping (i.e., the value of the coefficient 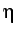 ) is strongly
problem dependent. For the simple 1-D problem at hand, the optimal
damping coefficients for the
) is strongly
problem dependent. For the simple 1-D problem at hand, the optimal
damping coefficients for the 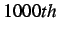 and
and 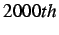 time step
insertion cases are
time step
insertion cases are 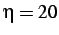 and
and 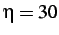 , respectively.
, respectively.
Figure 2.17:
Effect of cohesive damping: evolution of the displacement jump across the cohesive element for the simple 1-D test problem shown in Figure 2.14 and resulting from ``blind'' cohesive element insertion with damping at time 0,
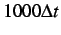 (
(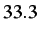
 ) and
) and
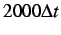 (
(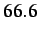
 ).
).
|
|
Furthermore, in 2-D, the presence of the damping term was found to be
much less effective in reducing the oscillations. These shortcomings
forced us to adopt another approach based on the pre-stretching of
the dynamically inserted cohesive elements. This approach is
described next.



Next: Cohesive Element Pre-Stretching
Up: Cohesive Element Stability and
Previous: Cohesive Element Stability and
Contents
Mariusz Zaczek
2002-10-13
![\includegraphics[scale=0.6]{dashpot1d.eps}](img187.png)
![]() ) is strongly
problem dependent. For the simple 1-D problem at hand, the optimal
damping coefficients for the
) is strongly
problem dependent. For the simple 1-D problem at hand, the optimal
damping coefficients for the ![]() and
and ![]() time step
insertion cases are
time step
insertion cases are ![]() and
and ![]() , respectively.
, respectively.
![\includegraphics[scale=0.6]{cohsep_blindinsertwithdamp_1d.eps}](img193.png)