


Next: Unequal Subcycled to Non-Subcycled
Up: Multi-Time Step Subcycling Results
Previous: Multi-Time Step Subcycling Results
Contents
We first test subcycling on an equal distribution of non-subcycled
and subcycled nodes, i.e. a region ratio of , with 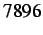 nodes,
nodes,
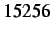 edges and
edges and 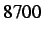 volumetric elements. Selecting a random node ahead
of the initial notch,
we plot its nodal displacements in
Figure 4.2 for the various
subcycling parameters. From this
figure we can see that subcycled solutions are very close to the
reference solution, although their accuracies decrease
with an increasing subcycling parameter.
volumetric elements. Selecting a random node ahead
of the initial notch,
we plot its nodal displacements in
Figure 4.2 for the various
subcycling parameters. From this
figure we can see that subcycled solutions are very close to the
reference solution, although their accuracies decrease
with an increasing subcycling parameter.
The timing results for the internal and cohesive force subroutines, the
main loop and the overall solution are presented in
Table 4.5.
As expected, the time for the internal force calculations decreases as the
subcycling parameter grows, although for
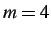 , the cost resulting
from the cohesive forces and main solution loop offsets the savings
of the internal forces - a
, the cost resulting
from the cohesive forces and main solution loop offsets the savings
of the internal forces - a 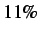 loss.
loss.
Figure 4.2:
Nodal displacements of a random node ahead of the notch for a problem with an equal region ratio () with subcycling parameters of
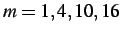 and
and 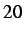 .
.
|
|
Table 4.1:
Timing results (in  ) for a problem with an equal region ratio () with subcycling parameters of
) for a problem with an equal region ratio () with subcycling parameters of
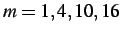 and
and 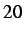 .
.
| Subroutine |
Reference Case [s], m = 1 |
m = 4 |
m = 10 |
m = 16 |
m = 20 |
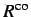 |
424.13 |
628.72 |
503.81 |
479.24 |
469.56 |
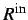 |
733.89 |
472.52 |
300.37 |
256.66 |
238.05 |
 |
427.29 |
652.91 |
499.89 |
469.59 |
439.78 |
 |
1628.54 |
1811.59 |
1359.70 |
1259.68 |
1201.80 |
   |
|
-11% |
17% |
23% |
26% |
|



Next: Unequal Subcycled to Non-Subcycled
Up: Multi-Time Step Subcycling Results
Previous: Multi-Time Step Subcycling Results
Contents
Mariusz Zaczek
2002-10-13
![]() , the cost resulting
from the cohesive forces and main solution loop offsets the savings
of the internal forces - a
, the cost resulting
from the cohesive forces and main solution loop offsets the savings
of the internal forces - a ![]() loss.
loss.
![\includegraphics[scale=0.6]{sub_case1d.eps}](img360.png)