


Next: Conclusions
Up: Dynamic Cohesive Node Insertion
Previous: Dynamic Insertion with Pre-Stretch
Contents
To further increase the time savings of our problem we combine
the dynamic cohesive node insertion and multi-time step subcycling
algorithms.
As a test case we chose a beam discretized into 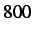 equal segments
of length =
equal segments
of length = 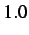
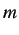 . Subcycling is
applied to the left and right regions with the subcycling parameter
. Subcycling is
applied to the left and right regions with the subcycling parameter
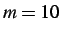 , as shown in
Figure 3.22. Cohesive nodes are dynamically
inserted at the
, as shown in
Figure 3.22. Cohesive nodes are dynamically
inserted at the 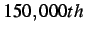 time step (
time step (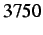
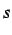 ), into the middle
), into the middle 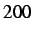 nodes, with
the simulation being run for
nodes, with
the simulation being run for 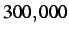 time steps (
time steps (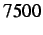
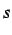 ) using a
) using a
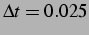
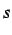 .
.
Figure 3.22:
Test case for dynamic insertion with subcycling.
|
|
Figure 3.23:
Velocity profile of node 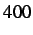 of dynamic cohesive node insertion at time step
of dynamic cohesive node insertion at time step 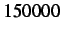 (
(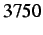
 ) with nodal subcycling using
) with nodal subcycling using
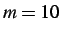 .
.
|
|
From Table 3.3 we can see that the combined
method, using dynamic insertion with subcycling, is more efficient
for the individual internal and cohesive force subroutines, although
the overall savings is minimal. This low time savings is due to the
costly implementation of the subcycling algorithm as well as the
increased number of nodal updates of the displacements, velocities
and accelerations in the main code.
Table 3.3:
Timing results for dynamic cohesive node insertion at time step  (
(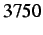
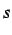 ) with nodal subcycling using
) with nodal subcycling using
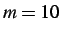 .
CPU time saving (in %) is given in parentheses.
.
CPU time saving (in %) is given in parentheses.
| Subroutine |
Reference Case [s] |
Combined Case,
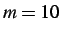 [s] [s] |
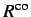 |
14.32 |
9.16 ( 36%) |
 |
27.33 |
15.93 ( 42%) |
 |
117.80 |
114.57 ( 3%) |
|



Next: Conclusions
Up: Dynamic Cohesive Node Insertion
Previous: Dynamic Insertion with Pre-Stretch
Contents
Mariusz Zaczek
2002-10-13
![\includegraphics[scale=0.6]{subandinsert.eps}](img337.png)
![\includegraphics[scale=0.6]{combined1d_mat.eps}](img338.png)