Formulation

As mentioned above, the backbone of this research is the CVFE scheme, which is schematically presented in Figure 2.1. It consists of a combination of conventional (volumetric) elements (represented by 3-node triangles in Figure 2.1, although most types of structural finite elements can be used) and of interfacial (cohesive) elements (represented by a 4-node element in Figure 2.1, although higher-order cohesive elements are also available). The volumetric elements are used to characterize the mechanical response of the bulk material, while the cohesive elements are introduced in the finite element mesh to simulate the spontaneous motion of one or more cracks in the structure. The capture of the failure process is achieved with the aid of a phenomenological cohesive failure law characterizing the evolution of the cohesive element response.

Figure 2.1: CVFE concept showing one 4-node cohesive element between two linear-strain triangular volumetric elements. The cohesive element is shown in its deformed configuration. In its undeformed configuration is has no thickness and the adjacent nodes are superposed.

The choice of the cohesive failure model plays an important role in the simulation of the fracture process. In this study, we use the bilinear rate-independent intrinsic formulation introduced by Geubelle and Baylor (1998), which is presented in Figure 2.2 for the pure mode I and mode II cases. The cohesive relation consists in two distinct portions: a linearly rising part, indicating an increasing resistance of the cohesive element to the separation of the adjacent volumetric elements, followed by a monotonically decreasing relation between cohesive traction and displacement jump simulating the progressive failure of the material. The maximum value of the normal ( $\sigma_{max}$) and tangential ( $\tau_{max}$) cohesive tractions respectively correspond to tensile and shear strengths of the material. Once the displacement jump ($\Delta _n$ for the tensile case and $\Delta _t$ for the shear case) has reached a critical value (respectively denoted by $\Delta_{nc}$ and $\Delta_{tc}$ for the mode I and II cases in Figure 2.2), the cohesive traction is assumed to vanish. No more mechanical interaction is then assumed to take place between the initially adjacent volumetric elements, thereby creating a traction-free surface (i.e., a crack) in the discretized solid domain.

Figure 2.2: Bilinear cohesive failure law for the pure tensile or mode I ( , left) and pure shear or mode II ( $\Delta _n = 0$, right) cases. An unloading and reloading path is also shown in the mode I case.

The area under the cohesive traction/separation curve correspond to the energy needed to generate a new fracture surface, i.e., the fracture toughness of the material, denoted by $G_{Ic}$ and $G_{IIc}$ for the modes I and II, respectively. To account for the possible coupling between the failure modes, the normal and tangential cohesive tractions, $T_n$ and $T_t$, are related to the norm of the displacement jump vector $\Delta = (\Delta_n, \Delta_t)$ through the introduction of the residual strength parameter $S$ defined as

$$\mathcal S = 1 - \Vert\tilde{\boldsymbol{\Delta}}\Vert.$$ (2.1)

where $\mathcal \Vert\tilde{\boldsymbol{\Delta}}\Vert$ denotes the Euclidean norm of the non-dimensional displacement jump vector $\tilde{\boldsymbol{\Delta}}$

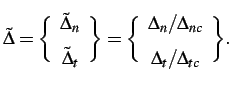$${\tilde{\boldsymbol{\Delta}}} = \bigg\{ \begin{array}{c} \tilde{\... ...in{array}{c} \Delta_n/ \Delta_{nc}\\ \Delta_t /\Delta_{tc} \end{array} \bigg\}.$$ (2.2)

To limit the detrimental effect that the compliance of the cohesive elements might have on the stress field solution, the residual strength parameter of a cohesive element is initially given a value $\mathcal S_{initial}$ very close to unity. Typically a value of $0.95$ to $0.98$ is used. As the element fails, this value progressively decreases to zero, at which point complete failure is assumed to have occurred. In order to maintain a monotonic decrease of this strength parameter and thereby prevent the possible healing of the cohesive elements, the minimum value achieved by ${\mathcal S}$ is stored at each integration point by using

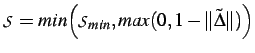$$\mathcal S = min\Big ( {\mathcal S}_{min}, max (0, 1 - \Vert\tilde{\boldsymbol{\Delta}}\Vert)\Big)$$ (2.3)

The resulting rate-independent coupled bilinear cohesive traction-separation law can be expressed as

$$T_n = \frac{\mathcal S}{1-\mathcal S}\tilde{\Delta}_n\sigma_{max}, \qquad \qquad T_t = \frac{\mathcal S}{1-\mathcal S}\tilde{\Delta}_t\tau_{max},$$ (2.4)

where

$$\tilde{\Delta}_{nc} = \frac{2G_{Ic}}{\sigma_{max}\mathcal S_{init... ...\Delta}_{nt} = \frac{2G_{IIc}}{\tau_{max}\mathcal S_{initial}}, \vspace*{0.5cm}$$ (2.5)

in which, as indicated earlier, $G_{Ic}$ and $G_{IIc}$ are the critical energy release rates (or fracture toughnesses) for mode I and mode II failures, respectively. The fracture mode coupling achieved by Equation 2.4 can be seen in Figure 2.3.

Figure 2.3: Coupled cohesive failure model described by Equation 2.4; variation of normal (top) and shear(bottom) cohesive tractions with respect to normal ($\Delta _n$) and tangential ($\Delta _t$) displacement jumps.