


Next: Stability and Mesh Size
Up: Review of the Cohesive/Volumetric
Previous: Formulation
Contents
The implementation of the CVFE scheme relies on the following form of
the principle of virtual work:
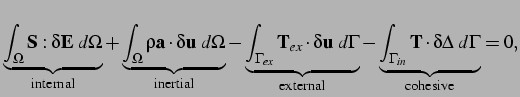 |
(2.6) |
where 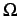 is the undeformed domain,
is the undeformed domain,
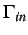 denotes the
interior ``cohesive'' boundary along which the cohesive tractions
denotes the
interior ``cohesive'' boundary along which the cohesive tractions 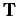 act, and
act, and
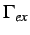 corresponds to the part of the exterior
boundary along which the external tractions
corresponds to the part of the exterior
boundary along which the external tractions
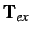 are applied.
are applied. 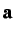 and
and 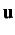 denote the acceleration and displacement fields,
respectively.
denote the acceleration and displacement fields,
respectively. 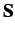 is the second Piola-Kirchoff stress tensor and
is the second Piola-Kirchoff stress tensor and
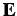 , the Lagrangian strain tensor, which is related to the
displacement field through
, the Lagrangian strain tensor, which is related to the
displacement field through
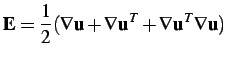 |
(2.7) |
Nonlinear kinematics is used in this study to account for the
possible large rotations present in the structure due to the fracture
process. The expression (2.6) of the principle of virtual work is
fairly conventional, except for the presence of the fourth term,
which corresponds to the virtual work done by cohesive traction 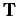 for a virtual separation
for a virtual separation
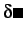 .
.
The resulting semi-discrete finite element formulation can be
expressed in the following matrix form:
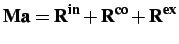 |
(2.8) |
where 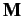 is the lumped mass matrix,
is the lumped mass matrix, 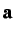 is the vector
containing the nodal accelerations, and
is the vector
containing the nodal accelerations, and
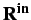 ,
,
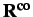 and
and
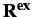 respectively denote the internal,
cohesive and external force vectors.
respectively denote the internal,
cohesive and external force vectors.
The time stepping scheme is based on the classical explicit
second-order central difference scheme (Belytschko et al., 1976):
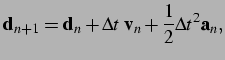 |
(2.9) |
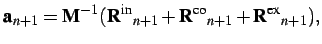 |
(2.10) |
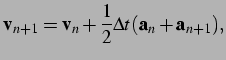 |
(2.11) |
where 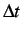 is the time step and
is the time step and
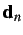 denotes the nodal
displacement vector at time
denotes the nodal
displacement vector at time
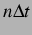 .
.
The expression of the internal, cohesive and external force vectors
can be found in Baylor (1997).While a variety of constitutive
models can be used to characterize the response of the volumetric
elements, we use, in this study, a simple linear isotropic relation
between the second Piola-Kirchoff stresses 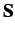 and the Lagrangian
strains
and the Lagrangian
strains 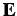 :
:
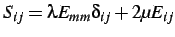 |
(2.12) |
where 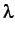 and
and 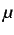 are the Lame's constants.
are the Lame's constants.



Next: Stability and Mesh Size
Up: Review of the Cohesive/Volumetric
Previous: Formulation
Contents
Mariusz Zaczek
2002-10-13
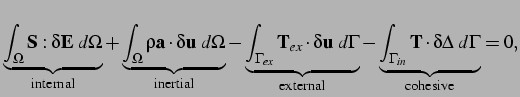
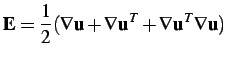
![]() for a virtual separation
for a virtual separation
![]() .
.
![]() and the Lagrangian
strains
and the Lagrangian
strains ![]() :
: