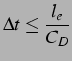Stability and Mesh Size

Like all explicit time stepping schemes, the central difference formulation is conditionally stable (Cook et al., 1989), and the time step size must satisfy the Courant (or CFL) condition:

$${\Delta t} \leq \frac{l_e}{C_D}$$ (2.13)

where $l_e$ is the smallest element size, $C_D$, the dilatational wave speed, given by

$$C_D = \sqrt{\frac{E(1-\nu)}{(1+\nu)(1-2\nu)\rho}}, \vspace*{0.5cm}$$ (2.14)

in which $E$, $\nu$ and $\rho$ denote the material's Young's modulus, Poisson's ratio and density, respectively.

In the region where failure is taking place, small elements have to be used to capture adequately the stress concentration associated with the presence of the crack front and the failure process. In particular, a sufficient number of elements (typically 5 to 10) must be used to discretize the cohesive zone, i.e., the region where cohesive failure is taking place. An estimate of the cohesive zone size can be obtained for the quasi-static mode I situation in terms of the constitutive and failure properties of the material, as

$$R = \frac{\pi}{8} \frac{E}{1-\nu^2} \frac{G_{Ic}}{{\sigma_{max}}^2}. \vspace*{0.5cm}$$ (2.15)

It is clear, however, that small elements must only be used in regions where failure is taking or is about to take place. A coarser discretization can be adopted in the rest of the domain, generating a possibly large disparity in element sizes, and therefore in time step sizes.

Furthermore, due to their inherent instability and to the need to accurately capture the failure process in the vicinity of the dynamically propagating crack front, the presence of cohesive elements in the discretized domain further reduces the time step size, typically to $1/30th$ of the Courant condition (Baylor, 1997).In an adaptive CVFE scheme where cohesive elements are only inserted in critical portions of the discretized domains, this additional time step requirement also suggests the need for time step subcycling.

In conclusion, the motivation for the incorporation in the CVFE scheme of the subcycling algorithm described in the next section can be schematically presented in Figure 2.4: time step disparity can be associated with spatial variations in element sizes (part a) and/or with the presence of cohesive domains (part b).

Figure 2.4: Time step defined by: (a) element size or (b) element type.